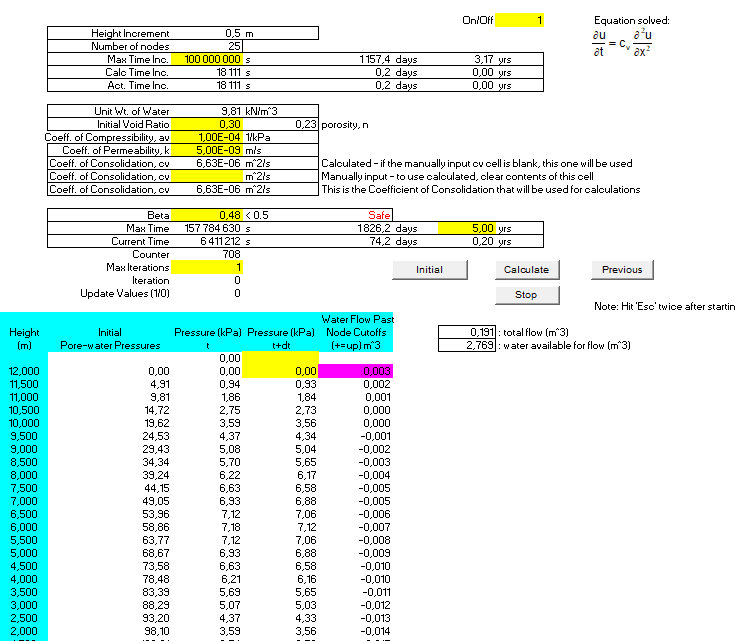
Finite Difference Solution to Terzaghi’s Consolidation Equation Spreadsheet

In the world of geotechnical engineering, understanding how soil behaves under the pressure of a new structure is paramount to ensuring its long-term stability. One of the foundational principles governing this behavior is Terzaghi’s Consolidation Equation. Developed by Karl Terzaghi, often hailed as the “father of soil mechanics,” this theory provides a mathematical framework for predicting the settlement of saturated clay soils over time.[1][2] This article will provide a comprehensive overview of Terzaghi’s one-dimensional consolidation theory, its practical applications, its limitations, and the modern advancements that build upon this fundamental concept.

What is Soil Consolidation?

Soil consolidation is the process of volume reduction in saturated soils, such as clays, due to the gradual expulsion of water from the pores under an applied load.[3][4] When a load, like a building foundation, is placed on a saturated clay layer, the initial pressure is carried by both the soil particles and the water within the pores. Since water is nearly incompressible, the initial pore water pressure increases significantly.[5][6] Over time, this excess pore water pressure dissipates as water drains out into more permeable layers, transferring the load to the soil skeleton and causing the soil to settle.[6][7] This time-dependent settlement is what Terzaghi’s theory helps us predict.[1]

Primary vs. Secondary Consolidation

It’s important to distinguish between the two main stages of consolidation:

• Primary Consolidation: This is the phase where settlement occurs due to the expulsion of pore water.[3][8] Terzaghi’s theory primarily focuses on this stage.

• Secondary Consolidation (or Creep): This phase begins after the excess pore water pressure has dissipated and involves the plastic rearrangement of soil particles under a constant effective stress.[8][9]

The Heart of the Matter: Terzaghi’s One-Dimensional Consolidation Equation

Terzaghi’s theory simplifies the complex process of consolidation into a one-dimensional problem, assuming that water flows and soil compresses only in the vertical direction.[5][10] The governing differential equation is analogous to Fourier’s law of heat conduction and describes how the excess pore water pressure (u) dissipates with time (t) and depth (z).[11][12]

The equation is:

∂u/∂t = c_v * (∂²u/∂z²)

Where:

• ∂u/∂t represents the rate of change of excess pore water pressure over time.[7]

• c_v is the coefficient of consolidation, a key parameter that reflects how quickly the consolidation process occurs.[1][7] A higher c_v indicates faster consolidation.[1]

• ∂²u/∂z² represents the rate of change of excess pore water pressure with depth.[7]

Key Assumptions of Terzaghi’s Theory

To make the complex reality of soil behavior manageable, Terzaghi’s theory is based on several key assumptions:[5][10][13][14]

1. Homogeneous and Fully Saturated Soil: The soil is assumed to have uniform properties throughout and to be completely saturated with water.[10][14]

2. Incompressible Soil Grains and Water: The solid particles and the pore water are considered incompressible.[10][14]

3. One-Dimensional Consolidation and Flow: Both the compression of the soil and the flow of water are assumed to occur only in the vertical direction.[10]

4. Darcy’s Law is Valid: The flow of water through the soil is assumed to be laminar and to follow Darcy’s law, which states that the flow rate is proportional to the hydraulic gradient.[10]

5. Constant Soil Properties: The coefficient of permeability and the coefficient of volume compressibility are assumed to remain constant throughout the consolidation process.[10]

6. Small Strains: The deformations are assumed to be small compared to the thickness of the consolidating layer.[9][10]

While these assumptions simplify the analysis, they also introduce limitations to the theory’s applicability in real-world scenarios.[7][13]

Practical Applications: Why Terzaghi’s Equation Matters

Despite its simplifying assumptions, Terzaghi’s theory remains a cornerstone of geotechnical engineering with numerous practical applications:[2]

• Settlement Prediction: The primary use of the equation is to predict the magnitude and rate of settlement of foundations, embankments, and other structures built on compressible soils.[2][15] This allows engineers to design foundations that can accommodate the expected settlement without compromising the structure’s integrity.[2]

• Foundation Design: By understanding the consolidation behavior of the underlying soil, engineers can select the appropriate type of foundation (e.g., shallow or deep) and design it to ensure long-term stability.[2][15]

• Construction Planning: The theory helps in estimating the time required for a significant portion of the settlement to occur, which is crucial for construction scheduling.[16] Techniques like preloading can be used to accelerate consolidation before the main construction begins.[3][15]

Limitations and Common Misconceptions

While invaluable, it’s crucial to recognize the limitations of Terzaghi’s theory:[7][13]

• Real Soil is Not Homogeneous: Natural soil deposits are often layered and heterogeneous, which is not accounted for in the theory.[7]

• Three-Dimensional Effects: In reality, consolidation and drainage can occur in three dimensions, especially near the edges of loaded areas.[7]

• Changing Soil Properties: The permeability and compressibility of soil can change as it consolidates.[17]

• Secondary Consolidation is Ignored: The theory does not account for secondary consolidation or creep, which can be significant in some organic soils.[9]

• Instantaneous Loading: The theory assumes the load is applied instantaneously, which is rarely the case in construction where loads are applied gradually.[7]

A common misconception is that the relationship between the degree of consolidation determined by pore water pressure and settlement is always linear.[18] However, experimental evidence has shown that this relationship can be non-linear.[18]

Beyond Terzaghi: Modern Advancements in Consolidation Theory

Recognizing the limitations of the classical theory, researchers have developed more advanced models to better simulate real-world conditions. These include:

• Two and Three-Dimensional Consolidation Theories: Biot’s theory provides a more rigorous framework for three-dimensional consolidation.[11][19]

• Non-Linear Consolidation: These theories account for the changes in soil properties during consolidation and can handle large deformations.[20][21] This is particularly important for very soft soils like dredged materials.[22][23]

• Consolidation of Unsaturated Soils: Modified theories have been proposed to analyze the consolidation of soils that are not fully saturated.[24][25]

• Numerical Methods: Finite element and finite difference methods allow for the analysis of complex geometries, non-linear soil behavior, and various boundary conditions that are difficult to solve analytically.[20][21]

Conclusion

Terzaghi’s Consolidation Equation remains a fundamental tool in the geotechnical engineer’s toolbox. It provides a crucial, albeit simplified, understanding of how saturated clays settle over time under load. While its assumptions may not perfectly mirror reality, the insights it offers into the time-dependent nature of settlement are invaluable for the safe and reliable design of structures. By understanding its principles, applications, and limitations, engineers can make more informed decisions and appreciate the advanced theories that continue to build upon this foundational work.

Download Link