Highway Design – Introduction to Horizontal and Vertical Alignment

 

The layout of a highway is comprised of two components: A horizontal component which is viewed from above and the vertical component which is viewed from the side.

The horizontal alignment dictates the left or right turning required to remain on the roadway, while the vertical alignment exerts forces on the vehicle as the grade along the roadway changes.

Horizontal Alignment:

In the horizontal perspective, a roadway is primarily comprised of tangent, or straight, sections which are smoothly connected by curves.

The horizontal curves that are used to provide drivers with the transition from one tangent to the next tangent are typically simple curves which are an arc of circle.

These curves have a single radius value which represents the sharpness or flatness of the curve.

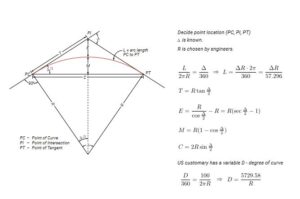
Highway Geometric Design – Horizontal Curve Equations

A tangent roadway section has an infinite radius, since it is a straight line and a horizontal curve has a single, finite radius. Therefore, a spiral transition is used in some instances to help make the shift from a tangent to a curve a little smoother.

Geometric relationships and equations can be used to find important information for reach curve. This information includes the radius, the length of the curve, the change in direction of the two tangents, and other factors depending on our needs.

Several points of interest along the curve include the location where the tangents intersect, which is known as the Point of Intersection. The location where the vehicle leaves the tangent section and begins to drive along the curve, is known as the point of curvature.

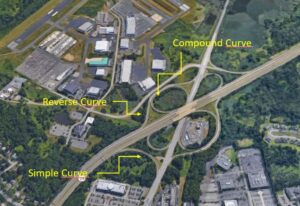
Types Of Horizontal Curves:

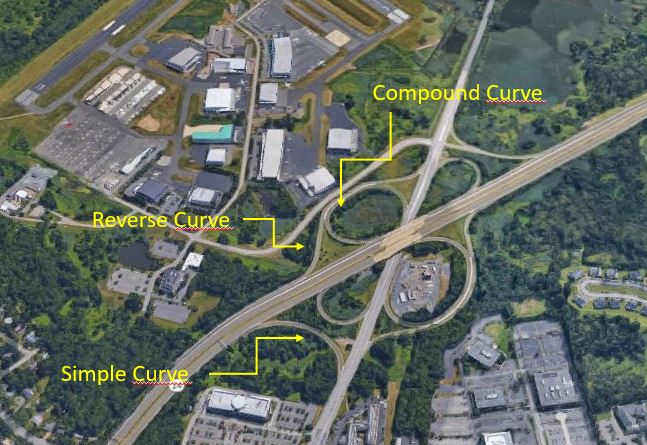
Horizontal curves are of different types as follows:

1.Simple circular curve

2.Compound curve

3.Reverse curve

4.Transition curve

 

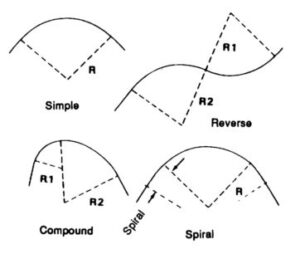
1. Simple Circular Curve

Simple circular curve is normal horizontal curve which connect two straight lines with constant radius.

2. Compound Curve

Compound curve is a combination of two or more simple circular curves with different radii. In this case both or all the curves lie on the same side of the common tangent.

3. Reverse Curve

Reverse curve is generated when two simple circular curves bending in opposite directions are meet at a signle point and that points is called as point of reverse curvature. The center of both the curves lie on the opposite sides of the common tangent such that the radii of both the curves may be same or different.

Types of horizontal curves

4. Transition Curve

A curve of variying radius is termed as transition curve. It is generally provided on the sides of circular curve or between the tangent and circular curve and between two curves of compound curve or reverse curve etc. Its radius varies from infinity to the radius of provided for the circular curve.

Transition curve helps gradual introduction of centrifugal force by gradual super elevation which provides comfort for the passengers in the vehicle without sudden jerking.

Spiral Curve

Spiral is a type of transition curve which is recommended by Indian Road Congress as ideal transition curve because of its smooth introduction of centrifugal acceleration. It is also called as clothoid.

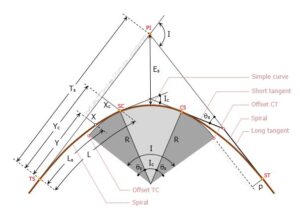
• TS = Tangent to spiral
• SC = Spiral to curve
• CS = Curve to spiral
• ST = Spiral to tangent
• LT = Long tangent
• ST = Short tangent
• R = Radius of simple curve
• T_s = Spiral tangent distance
• T_c = Circular curve tangent
• L = Length of spiral from TS to any point along the spiral
• L_s = Length of spiral
• PI = Point of intersection
• I = Angle of intersection
• I_c = Angle of intersection of the simple curve
• p = Length of throw or the distance from tangent that the circular curve has been offset
• X = Offset distance (right angle distance) from tangent to any point on the spiral
• X_c = Offset distance (right angle distance) from tangent to SC
• Y = Distance along tangent to any point on the spiral
• Y_c = Distance along tangent from TS to point at right angle to SC
• E_s = External distance of the simple curve
• θ = Spiral angle from tangent to any point on the spiral
• θ_s = Spiral angle from tangent to SC
• i = Deflection angle from TS to any point on the spiral, it is proportional to the square of its distance
• i_s = Deflection angle from TS to SC
• D = Degree of spiral curve at any point
• D_c = Degree of simple curve

Bernoulli’s lemniscate

In this curve, the radius decreases as the length increases and this causes the radial acceleration to keep on falling. The fall is, however, not uniform beyond a 30 o deflection angle. We never use this type of curve on railways.

 

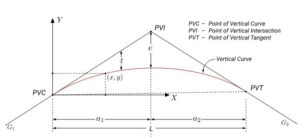
Vertical Alignment:

 

In the vertical perspective, a roadway is also comprised of tangents which are smoothly connected by curves. For vertical alignment, the tangents represent grades which can either be flat, uphill or downhill.

The typical vertical curve is a symmetric, parabolic curve whose shape is defined by the parabolic equation.

The information required to fully define a vertical curve is the elevation of the beginning of the curve, the grades of the two tangents that are connected ad the length of the curve.

The naming convention of vertical alignment is similar to horizontal alignment. Several points of interest along the curve include that the location where the tangents intersect, which is known as the Point of Vertical Intersection.

The location where the vehicle leaves the tangent grade and begin to drive along the curve, is known as the point of vertical curvature.

The point where the curve ends and the vehicle returns back to the tangent grade is known as the Point of Vertical Tangency.

Highway Geometric Design – Vertical Curve Equations

 

Types Of Vertical Curves:

In general parabolic curve is preferred as vertical curve in the vertical alignment of roadway for the ease of movement of vehicles. But based on the convexity of curve vertical curves are divided into two types

1.Valley curve

2.Summit curve

1. Valley Curve (sag curve)

Valley curve connects falling gradient with rising gradient so, in this case convexity of curve is generally downwards. A second name for valley curve is sag curve.

They are formed when two gradients meet as any of the following four ways:

• When a negative gradient meets another mild negative gradient
• When a negative gradient meets a level zero gradient
• When a negative gradient meets with a positive gradient
• When a positive gradient meets another steeper positive gradient

2. Summit Curve (crest curve)

Summit curve connects rising gradient with falling gradient hence, the curve has its convexity upwards. A second name for summit curve is crest curve.

They are formed when two gradients meet as in any of the following four ways:

• When a positive gradient meets another positive gradient.
• When positive gradient meets a flat gradient.
• When an ascending gradient meets a descending gradient.
• When a descending gradient meets another descending gradient.

Suggested Read:

Why Are Spiral Curves Important? Benefits And Elements Of Spiral Curve